* 기동시의 에너지 *

  항공기의 성능을 나타내는 자료들에서 추력중량비라는 말을 들어보신 적이 있을 겁니다. 말 그대로 엔진 추력을 항공기 중량으로 나눈 값입니다. 이 값이 1보다 크면 수직으로 상승하면서 가속을 할 수 있다는 뜻입니다. 전투기동시의 에너지도 추력과 밀접한 관련이 있습니다. 그런데, 이 추력 중량비는 변수가 너무 단순해서 실제 전투기동을 분석하는 데에는 별 도움이 안되고 아주 일반적인 기체 성능의 한가지 참고자료로서만 쓸 수 있습니다. 그 대신 공중전 역학을 이야기할 때에는 이 공식에 실제적인 변수를 더 추가한 잉여추력(Specific excess Power)이라는 개념을 이용합니다. 간단하게 말하면 이 개념은 추력과 항력을 비교하여, 추력의 여분이 얼마나 있는지를 판단하는 것입니다. 당연히 높을수록 좋겠죠. 이번에는 공식부터 보겠습니다.

 잉여 추력 (Ps) = V (T-D) / W       (단위: ft/sec)
V: 속도
T: 추력
D: 항력
W: 중량

 이를 글로 풀어서 쓰면 이렇습니다.
 높은 잉여추력을 얻기 위해서는 중량은 작아야 하고, 엔진 추력은 높아야 하고, 항력은 작아야 하고, 속도는 높아야 한다는 것입니다. 이 변수들은 모두 기체 자체의 성능에 기본적으로 영향을 받지만, 비행 상황에 따라서 바뀔 수 있고 조종사가 어느정도 제어할 수 있습니다.
 이 잉여추력 공식 역시 전자계산기로 계산하면서 비행하기 위해 필요한 것이 아니라, 각 변수들이 에너지 관리에 어떻게 영향을 미치는지 원리를 알기 위해 설명드린 것입니다. 전투기동을 하면서 에너지 우세를 달성하고자 한다면 잉여 추력율이 높아지는 방향으로 속도, 추력, 항력, 중량 등의 변수들을 제어하면 되는 것이지요. 잉여 추력값은 크게 0보다 크거나, 0보다 작거나, 0과 같다는 세 가지 경우로 구분할 수 있습니다. Ps > 0 에서는 가속을 하거나 혹은 상승을 할 수 있고, Ps < 0 에서는 속도나 고도를 상실하게 됩니다. Ps=0이라면 현재의 고도와 속도를 유지하면서 현재의 기동을 계속 할 수 있다는 것입니다. 즉, Ps값이 0이거나 그 이상인 영역 내에서의 가장 높은 선회율이 곧 "최대 지속 선회율"이 되는 것입니다. 가능하다면 자신이 몰고 있는 비행기의 기본적인 Ps값 데이터를 알고 있으면 좋겠지만, 모르더라도 기동을 하면서 어느정도 감으로 느낄 수 있습니다.

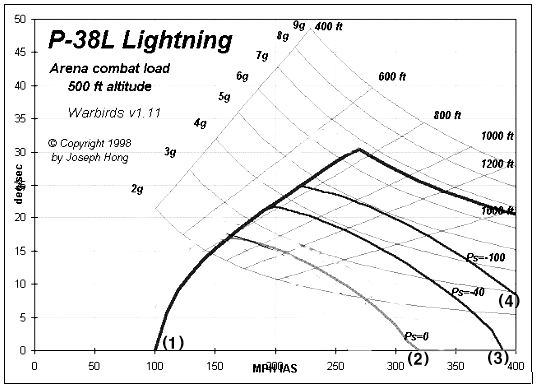
 이 Ps값도 E-M 차트에 함께 표시가 됩니다. 앞서 보여드린 F-16A Block15의 차트는 설명 순서상 Ps값이 표시되지 않은 자료로 설명드린 것이고, 원래는 그래프의 이름에도 나와있다시피 기동에 따른 에너지 변화율을 나타내는 Ps값까지 함께 볼 수 있도록 하는 것이 E-M 차트의 본래 기능입니다. 다음 그래프는 고도 500피트에서의 전투중량의 P-38L형의 E-M 차트입니다.

 먼저 기본 비행 성능부터 보겠습니다. 그림에서 P-38L형의 비행성능 한계는 속도 100노트에서 시작하는 가장 굵은 실선(1번 선)으로 표시되어있습니다. 주요 수치들을 읽어보자면, P-38은 주어진 고도에서 6.8G까지 당길 수 있고, 최소선회반경은 약 760피트입니다. 1번 선의 왼쪽 끝인 속도 100노트가 해당 고도에서의 실속 속도입니다. 원래는 데이터가 오른쪽으로도 더 있지만 그래프에서는 데이터의 오른쪽 부분이 짤려있기 때문에 최대속도는 알 수 없습니다. 1번 선의 Y축 최고점이 최대 선회율이며, 이 점에서 이 항공기의 코너스피드는 270노트, 이때 당길 수 있는 G는 6.8G, 선회반경은 760피트를 가지게 되고 이 때 최대 선회율은 초당 약 30도입니다.

흐린 선은 P-38의 비행한계와는 상관 없는 기본 선회반경 그래프와 G 그래프의 선들입니다. 이 선들은 성능을 나타내는 것이 아니라 수치를 읽는 참조점으로만 쓰입니다.

 이제 잉여 추력(Ps) 값에 대해 설명드리겠습니다. 이 그래프에서 Ps값을 나타내는 선들은 굵은 실선 아래에서 오른쪽 아래로 흐르는 실선, 즉 2,3,4번 선들입니다. Ps=0을 기준으로 에너지가 남느냐 모자라느냐를 구분하는 것이 가장 중요하므로, 중요하게 보아야 할 것은 Ps=0인 2번 선입니다. 2번 선의 오른쪽 위에서는 기동시 에너지가 감소되며 왼쪽 아래에서는 에너지가 남습니다. 따라서,  그래프의 주인공인 P-38L형으로 에너지를 상실하지 않는 최대 기동성은 Ps=0 선이 최고점이 되는 부분입니다. 그래프에서는 1번 선과 2번 선이 만나는 지점이 Ps=0의 최고점이므로, 이 지점의 수치가 P-38의 최대 지속 선회성능입니다. 수치를 읽어보자면 속도는 160노트, 이때 당길 수 있는 G는 2.5G, 선회율은 초당 17도를 얻을 수 있습니다.

  코너속도인 270노트에서 이 비행기가 당길 수 있는 최대 G인 6.8G를 당기면 순간적인 최대 선회율을 얻을 수 있지만, 그 지점에서는 Ps<0이므로 속도가 줄어들게 되고 그러면 선회율 역시 줄어듭니다. 만약 코너속도에서 최대 G로 기동을 했다고 가정하면, 비행기의 비행수치는 1번 선의 최고 정점에서부터 1번 선을 따라 점차 내려오고(즉 속도와 선회율이 줄어들고) Ps=0인 점에서 더 이상 속도가 줄지 않게 되므로 선회율도 더 떨어지지 않고 일정하게 유지됩니다.

 보시다시피 P-38L형의 비행가능 영역 중 에너지를 상실하지 않고 기동할 수 있는 범위는 상당히 제한됩니다. 최대로 5.7G를 당길 수 있는 비행기에서 지속적으로 선회할 수 있는 에너지를 유지하기 위해서는 2.5G 이상을 당기지 말아야 한다고 하면 의외로 낮은 수치지요. 이는 프로펠러기의 추력이 그만큼 부족하기 때문입니다. 추력이 강한 비행기일수록 이 Ps>0의 영역이 넓어집니다. 기종간의 구체적인 수치 차이는 있지만, 2차대전급의 프로펠러 전투기들은 대체로 이러한 패턴의 E-M 차트를 가집니다. 2차 대전 전투기들은 이렇게 3G정도만 당겨도 에너지를 잃어 버리고 기동성이 둔화되어 버릴 정도로 기동 중의 에너지 손실이 컸기 때문에 2차 대전의 프로펠러 전투기들에서 특별히 불가피한 경우가 아닌 한 전투시에 지속적인 적기와의 꼬리잡기 선회가 권장되지 않은 것이죠. 그래서 그것이 2차 대전 전투기의 전투전술이 에너지 손실을 감수하는 선회전과 일격이탈 전술로 크게 양분되는 원인이 되었습니다.

 어떤 기종이든 E-M 차트의 비행 한계 영역의 형태는 삿갓 모양으로 비슷합니다. 그렇지만, 잉여 추력 곡선은 기종에 따라 몇 가지의 다른 형태를 가지고 있습니다. 잉여 추력 곡선의 패턴이 다르면 그에 따라서 에너지를 고려하여 기동하는 패턴도 달라지게 되므로, 잉여 추력 곡선의 패턴을 몇 가지 더 보여드리겠습니다.

 
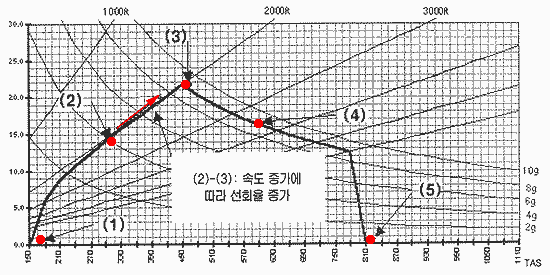
F-16 초기형의 E-M 차트

 위 그래프는 초기형 F-16의 어떤 고도에서의 E-M차트입니다.

 그림을 보시면, 굵은 실선의 그래프 상에 5개의 붉은 점이 보입니다. 이를 편의상 왼쪽부터 1,2,3,4,5범 점이라고 이름을 붙였습니다.

각 점들을 설명하면 다음과 같습니다. 이 그래프에서는 Ps 곡선은 생략되어있지만, 붉은 점들 중에 Ps=0이 비행 영역과 만나는 점들이 있으므로 그 점들을 기준으로 설명드리겠습니다.

1번: 실속 속도.

2번: Ps=0인 점.

3번: 최대 순간 선회율을 나타내는 점, 즉 코너 속도.

       여기서는 코너속도가 460노트, 이 때 9G로 초당 21도의 선회율을 얻을 수 있습니다.

4번: 이전의 P-38 차트에서는 없었던 점입니다.

       이역시 Ps=0값인 점인데 나중에 자세하게 설명하겠습니다.

5번: 최대 속도

 다른 점들의 의미는 P-38에서와 같고, P-38L형의 차트에는 에는 나타나지 않았던 4번 점에 대해서 설명드리겠습니다.

 잉여 추력을 구할 때 추력이 분자에 위치하므로, Ps값은 추력이 높을수록 증가합니다. P-38L형의 경우에는 프로펠러기이므로 추력이 매우 부족하여 Ps=0선이 최고점에서부터 우측 아래로 쳐졌으나, 제트기인 이 비행기는 추력이 높으므로 Ps=0선이 오른쪽 아래로 쳐지지 않고 2번 점에서부터 오른쪽으로 가면서 오히려 위쪽으로 상승하여  에너지를 유지하면서 기동할 수 있는 영역이 증가하였습니다. 그리고 다른 조건이 같을 때 속도가 높으면 Ps값의 증가 요인이 되므로, 2번에서 Ps값과 기동영역이 한번 만난 후 높은 추력에 덧붙여 속도가 높아짐으로 인하여 Ps값이 오히려 증가하여 다시 Ps=0값과 기동영역 한계가 만나게 된 것입니다.

이때, 프로펠러기와는 약간 다른 에너지 관리에 대한 생각이 가능합니다. 즉,  이 전투기에서는 에너지를 유지하며 최대 선회율로 선회할 수 있는 점이 2번 점보다 4번 점이 더 높은 Y축 수치를 나타내므로 4번 점이 에너지를 유지하면서 최대 선회를 할 수 있는 "최대 지속 선회율"을 나타내는 점이 됩니다. 물론, 코너속도인 3번 점에서 최대 순간 선회율로 선회를 하면 속도가 점차 떨어져 2번 점에서 지속 선회율이 나옵니다. 하지만 이렇게 얻어지는 지속 선회율은 P-38에서와는 달리 이 비행기의 최대 지속 선회율 값이 아닙니다. P-38에서는 조금이라도 급격한 전투기동을 하면 무조건 에너지가 떨어질 것을 감수할 수밖에 없고 스틱을 세게 당기더라도 어차피 최대 지속 선회율 값으로 비행 수치가 수렴하지만, 이 비행기에서는 어느 정도의 전투기동을 하면서도 상대적으로 높은 지속 선회율을 유지할 수 있습니다. 특히 4번 지점에서는 최대 G 한계에서 Ps=0이므로, 4번 지점인 600노트 이상의 속도에서는 최대한의 급격한 기동을 하더라도 에너지를 손실하지 않습니다. 제트기 시뮬레이션을 하다보면 코너 속도 부근의 중저속에서는 높은 G를 당기면 에너지가 감소하는데 고속에서는 높은 G를 걸어도 속도가 오히려 증가하는 현상을 발견할 수 있는데, 바로 이렇게 속도 증가가 잉여 추력 증가의 요인이 되기 때문에 그렇습니다. 이렇게 높은 속도에서 근접 전투기동을 계속 하고자 한다면 스로틀을 줄이거나 고도를 높여서 속도를 줄여야만 합니다.

 P-38의 E-M 차트와 이 그래프에서의 Ps값이 0 이상인 영역의 비율을 비교해보면 높은 엔진 추력이 전투기의 전반적인 기동 성능에도 얼마나 막대한 영향을 끼치는지 잘 알 수 있습니다.

  2번 지점은 비교적 낮은 G(4G)를 당기면서 초당 14도의 선회율을 얻으므로 조종사의 부담이 적은 반면 속도가 낮으므로 전술적으로 불리하고, 기동을 부드럽게 줄이지 않는 한 가속능력이 상대적으로 떨어집니다. 이정도로 속도가 낮아지면 아무리 스틱을 세게 당겨도 높은 G를 얻을 수 없으므로 블랙아웃에 빠질 위험은 적어집니다. 그러나 느린 속도에서는 스틱을 세게 당긴다고 해서 전투기가 급격하게 기동하고 있는 것이 아니라는 것을 잊지 말아야 합니다. 에너지 개념이 부족한 많은 조종사들이 무작정 스틱만 세게 당기고 있으면서 속도가 현격하게 느려졌는데도 최선의 급격한 전투기동을 하고 있다고 착각하곤 합니다. 그러나 실제로는 9G를 낼 수 있는 전투기에서 불과 3-4G밖에 안되는 기동을 하고 있는 것이죠. 결과는? 죽음입니다. 그렇게 때문에 무작정 스틱을 당기는데만 급급하지 말고 급격한 기동을 할 수 있는 충분한 속도가 있는지 항상 생각해야 합니다. 기동에 필요한 에너지를 잃지 않는 것이 기동 그 자체를 위해서도 굉장히 중요합니다.

 반면, 4번 지점은 속도가 높으므로 에너지가 충분하고 4번 점의 속도 이상에서는 얼마든지 G를 당겨도 되므로 에너지 유지관리에 훨씬 유리하지만, 높은 속도에서는 선회반경이 커지고 같은 선회율을 얻기 위해서도 상대적으로 높은 G를 당겨야 하고 조종사에게 부담이 되기 때문에 실제로 높은 속도에서 급격한 기동을 하기에는 많은 무리가 따릅니다. 팰콘 4.0을 보면, 근접 전투기동중 블랙아웃에 지나치게 잘 빠진다면 스틱을 너무 심하게 당겨서가 아니라 지나치게 속도를 높이고 이를 제어하지 못하기 때문인 경우가 많습니다. 예를 들면, 코너속도보다 높은 500노트의 속도에서 부드러운 스플릿 S를 한다면 속도가 걷잡을 수 없이 높아져 버리게 되겠죠. 일단 한번 4번 점까지 속도가 높아지고 나면 아무리 급격하게 기동을 하더라도 속도가 줄지 않기 때문에, 상승을 하거나 스로틀을 줄이는 등 속도 관리를 위한 조치를 취하지 않으면 아무리 스틱을 세게 당기더라도 조종사에게 고통만 가해질 뿐 선회율은 점점 더 낮아지고 선회반경은 대폭 커지게 됩니다. 이렇게 지나치게 높은 속도에서 급기동으로 적의 꼬리를 물고자 움직인다면 같은 비행기를 타고 똑같이 최대 기동능력인 9G를 당기더라도 더 낮은 속도에서 좁은 선회반경으로 기동하는 상대에 대해서 속수무책으로 당할 수밖에 없게 됩니다. 결과는 역시 죽음입니다. 무작정 스틱만 세게 당긴다고 다가 아니듯이, 스로틀을 무작정 최대로 올려놓고 있는 것도 다가 아닙니다.

 따라서 넓게 보면, 조종사는 낮은 G를 감수하면서 상대적으로 느린 속도로 기동하거나, 아니면 높은 속도를 유지하면서 높은 기동 잠재력을 유지하는 게임플랜을 선택할 수 있습니다. 물론 어느 한가지 게임 플랜이 항상 최선은 아닙니다. 여러 가지 전투상황에 따라서 적합한 방법들이 존재합니다. 다만, 똑같은 선회율로 선회를 했다고 하더라도 저속에서 선회를 했을 때에는 가진 에너지가 작고 높은 속도로 선회했을 때에는 여전히 높은 에너지를 가지고 있는 것이므로 에너지 여유를 가지고 있는 것이 그만큼 융통성 있고 기동의 잠재력이 더 높다고 할 수 있습니다.

 다음의 그래프는 팰콘4.0 매뉴얼에 나오는 F-16C Block 50의 고도 15,000 피트에서의 E-M 차트입니다. 이 그래프가 비행 한계 영역과 잉여 추력이 제대로 그려져 있는 완전한 형태의 E-M 차트입니다. 여기에는 하나의 그래프에 속도, 선회율, 선회반경, G, 잉여 추력의 다섯 가지의 수치가 들어있고, 이 다섯 가지의 비행 수치 중 어떤 두 가지를 알면 그래프의 한 점을 찾을 수 있고 그러면 나머지 세 가지 수치도 알 수 있습니다. 예를 들면, 마하 0.8의 속도로 5G를 당긴다고 하면 X축에서 마하 0.8과 G 곡선의 5G가 만나는 점을 찾아서 다른 수치들을 읽으면 됩니다. 이 예에서는 선회율은 초당 약 11도, 선회반경은 약 4500피트, 잉여 추력은 약 380이 됩니다.

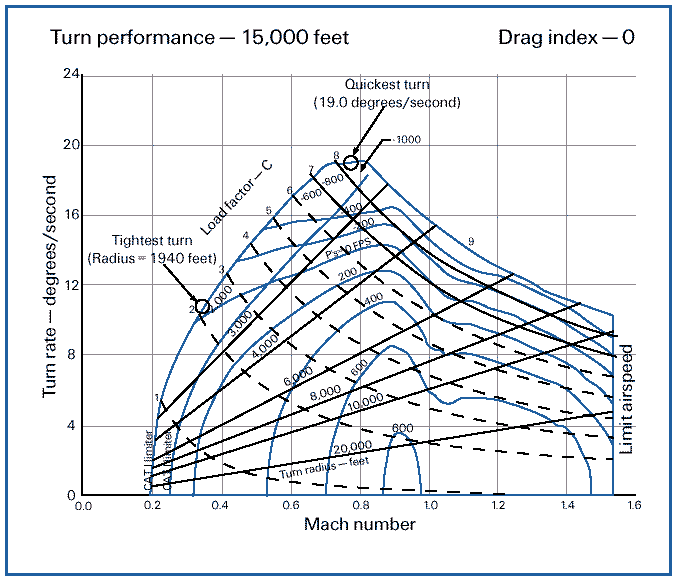
F-16C Block 50의 E-M 차트

 이 그래프를 보면 지속 선회 게임플랜과 순간 선회 게임플랜의 차이를 명확하게 알 수 있습니다. 최대 지속 선회율은 Ps=0인 영역이 Y축에서 가장 높은 지점에서 얻어지므로, 여기서는 마하 0.9에서 초당 14도가 이 비행기의 최대 지속 선회율입니다. 이를 위해서는 7G를 당겨야 합니다. 그리고, 최고 순간 선회율은 마하 0.7~0.8 사이의 속도에서 9G를 당길 때 초당 19도입니다. 이 비행기로 최대한의 급격한 선회를 하면 9G로 최대 초당 19도의 선회를 하지만, 그렇게 기동하면 Ps<0이 되므로 속도가 떨어지고, 속도가 떨어짐에 따라 선회율도 같이 떨어져서 Ps=0이 되는 지점에서 속도와 선회율이 고정됩니다. 이 때 유지되는 비행 수치는 2G, 지속되는 선회율은 초당 10도입니다. P-38에서는 최대한의 급기동을 하더라도 어차피 최대 지속 선회율 값으로 속도와 선회율이 수렴되므로 선택의 여지가 없었습니다. 그렇지만, 여기서는 속도를 마하0.9로 유지하고 7G를 당겼을 때는 초당 14도를 얻을 수 있으나 최대한의 급기동을 하면 결국에는 불과 2G의 초당 10도밖에 얻지 못합니다. 때문에 꼬리물기 선회가 길어지는 경우라면 최대한의 급기동을 하는 것이 오히려 선회율을 떨어뜨리는 결과가 되고, 이를 방지하기 위해서는 충분한 속도로 기동에 임하고 지나치게 스틱을 세게 당기지 말아야 합니다. 위의 그래프는 F-16C Block 50형의 예이지만, 지속적으로 일정한 선회율을 얻기 위해서는 스틱을 당기는 정도를 최적화시켜야 한다는 역학적 원리는 프로펠러기를 포함한 모든 비행기가 다 마찬가지입니다. (프로펠러기에서도 스틱을 덜 당기면 에너지의 손실비율을 줄일 수 있습니다.)

 전투기의 코너 속도, 잉여 추력율 등은 드문 경우 각 기종들의 데이타를 구해볼 수 있긴 하지만, 전투기의 구체적인 데이터, 특히 현재 운용되고 있는 항공기 데이터의 상당부분은 군사기밀에 속하기 때문에 구체적인 데이타를 구하기는 상당히 힘듭니다. 그 대신, 주어진 시뮬레이션에서 고도당 최대 선회율을 나타내는 속도, 최대 G를 당기면서 에너지를 상실하지 않는 속도등은 시험비행에 의한 실험값으로 근사치를 구할 수 있으므로 이를 플레이에 참고자료로서 사용할 수 있습니다. 최대 속도와 최소 속도는 쉽게 알 수 있고, 코너 속도도 게임에서 실험값으로 구해볼 수 있습니다. 일단 충분히 높은 속도를 얻은 후 스틱을 끝까지 당겨서 수평 선회를 하며 G메터의 수치를 보고, 속도가 줄어듦에 따라 어느 속도에서 현재 당기고 있는 G 수치가 떨어지기 시작하는지를 보면 됩니다. 이 때 당기고 있는 최대 G 수치가 떨어지기 시작하는 지점이 코너 속도입니다. 혹은 G메터가 없는 경우에는 같은 방법으로 기동하면서 G메터를 보지 않고 헤딩 변화율을 어림짐작으로 추산해서, 헤딩의 변화율이 가장 빠른 속도가 얼마인지를 보아도 코너 속도를 대략적으로 짐작할 수 있습니다. 그리고 잉여 추력은 여러 속도대에서 고도를 일정하게 유지하고 최대 출력으로 선회하면서 어느 정도로 G를 당겼을 때 속도가 떨어지기 시작하는지를 파악해보면 대략적인 값을 알 수 있습니다.

 공중전투 메뉴로  | 앞 페이지로  |  맨 위로  |  다음 페이지로