* 선회반경과 선회율 *

 전투기동이란 적기가 나를 쏘지 못하게 하고 내가 적기를 쏠 수 있기 위해 적기의 후방을 차지하고 내 비행기의 기수를 적기를 향할 수 있게끔 움직이는 것을 말합니다. 이에 대해 적기 역시 가만히 앉아서 죽어주지는 않고 똑같은 목표를 위해 기동할 것이므로, 이 목표를 이루려면 적기보다 더 효과적으로 기동을 해야 합니다. 단, 효과적으로 기동한다는 것이 단지 스틱을 무조건 세게 당긴다는 의미는 아닙니다. 앞서 간단하게 언급한 바와 같이 전투 기동에는 에너지와 각도를 비롯한 여러 가지 복잡한 변수들이 영향을 미치기 때문에, 이 변수들을 적절히 제어해야 효과적으로 기동을 할 수 있습니다. 그리고 그를 위해서 전투기의 기동에 대한 역학적인 이해가 필요합니다.

 전투기의 선회능력을 이야기하는 두 가지의 개념이 있습니다. 하나는 선회반경이고, 다른 하나는 선회율입니다. 선회반경은 내 비행기가 선회하고 있는 비행경로의 폭을 말합니다. 더 좁은 선회반경으로 선회를 하면 적기가 내 선회반경의 안쪽으로 파고들어와서 무기를 발사하지 못하겠지요. 선회율은 내 비행기의 기수가 얼마나 빠른 비율로 회전하는가 하는 것을 말합니다. 적기 쪽으로 기수를 빠르게 돌릴 수 있다면 그만큼 적에게 무기를 발사할 기회를 더 빨리 얻을 수 있을 것입니다. 선회반경과 선회율은 속도와, 스틱을 얼마나 당기느냐에 달려있습니다. 다음 그림들은 전투기동시에 더 좁은 선회반경과 더 높은 선회율이 각각 어떤 유리성을 제공하는지를 보여줍니다.

 좁은 선회반경의 이점                                           높은 선회율의 이점
 

 선회반경은 속력이 낮을수록 좁아집니다. 빠르게 달리는 자동차는 좁은 반경으로 선회할 수 없지만, 거의 정지해있는 자동차는 아주 좁은 반경으로 차를 돌릴 수 있는 것과 마찬가지의 원리입니다. 속력이 높아질수록 선회반경은 기하급수적으로 넓어집니다. 그리고, 선회반경은 또한 당기는 G의 영향을 받습니다. 자동차의 핸들을 더 많이 꺾으면 자동차가 더 좁게 선회를 하듯이, 스틱을 더 세게 당길수록 비행기의 선회반경은 더 좁아집니다. 정확하게 말하면, 선회반경은 속력의 제곱에 비례하고 당기는 G(하중계수)에 반비례합니다. 이를 한눈에 보기 쉽게 수학식으로 표시해보면 다음과 같습니다.

선회 반경 (Turn Radius) = V² / G
(G=하중계수, V = 속력)

 그래프로 표시하면 다음과 같습니다.

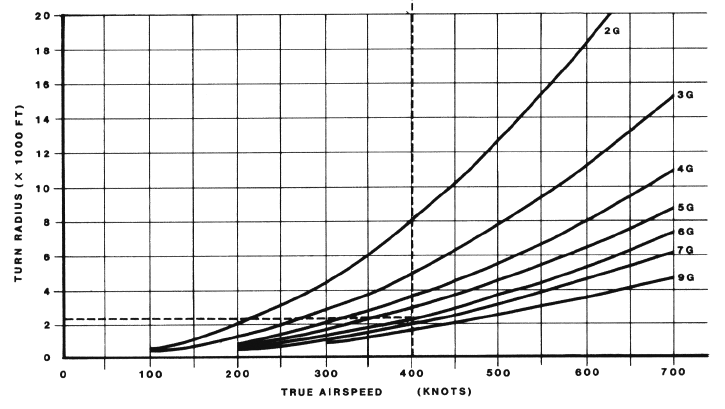
속도와 G에 따른 선회반경

 선회율은 당연히 당기는 G가 높아질수록 높아지고, 같은 G를 당긴다면 같다면 속력이 높아질수록 낮아집니다. 선회율 역시 선회반경을 설명할 때 자동차의 선회를 예로 든 것과 마찬가지 원리입니다. 이것도 식으로 표시해보죠.

선회율(Turn Rate) = G / V            단위: 도/초

또, 그래프로 그려보면 이렇습니다.

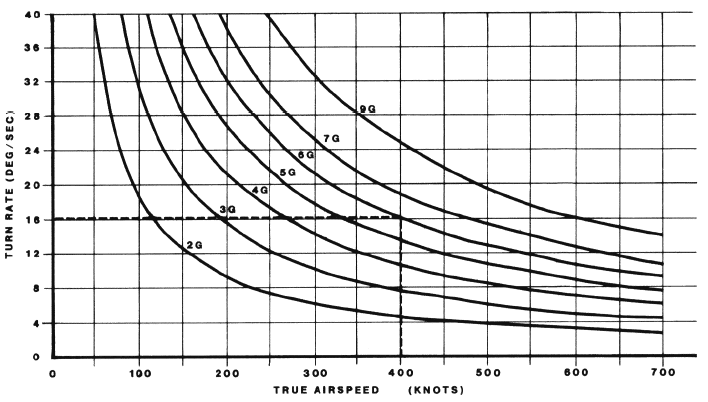
속도와 G에 따른 선회율

 공식이나 그래프가 나온다고 해서 걱정하실 필요는 없습니다. 비행을 하면서 전자계산기를 두드리실 필요는 없고, 단지 속도와 G가 선회반경과 선회율에 어떻게 영향을 미치는지 그 기본 원리만 이해하시면 됩니다.
 이상에서, 적기보다 더 선회를 잘 하기 위해 선회반경은 좁히고 선회율은 높이려면, G는 가급적 높이고 속력은 가급적 늦추면 된다는 것을 알 수 있습니다. 그런데 한가지 문제가 있습니다. 자동차는 거의 정지한 상태에서도 핸들을 끝까지 꺾을 수 있지만, 비행기는 그렇지 못합니다. 속력이 빠를수록 더 많은 양력을 얻을 수 있다는 것을 말씀드린 적 있을 것입니다. 즉, 낮은 속력에서는 높은 G를 당길 수 없고, 속력이 높아져야 더 높은 G를 당길 수 있습니다. 이는 비행 인벨롭 그래프에서 보신 바와 같습니다. 속력이 높아야 더 높은 G를 당길 수 있는데, 같은 G라면 속력이 높아지면 선회율이 낮아지고 선회반경이 커지기 때문에 속력은 선회율과 선회반경에 반대효과를 미칩니다. 그러면 결국 속력을 늦춰야 하느냐 높여야 하느냐의 문제가 생기게 됩니다. 이의 해결답안은 이렇습니다. 어떤 비행기가 당길 수 있는 최대 G는 한계가 정해져있습니다. 이 최대 G를 당길 수 있을 만큼의 충분한 속력이 있어야 하고, 그 조건하에서는 가장 낮은 속력을 가지고 있어야 합니다. 이 속도에서 선회율은 최대가 되고 선회반경은 최소가 됩니다. 이렇게 어떤 비행기가 최고의 선회율을 얻을 수 있는 속도를 코너 속도(Corner velocity 혹은 Corner speed)라고합니다. 자신의 비행기를 효과적으로 다룰 수 있으려면 자신의 비행기의 코너속도를 비롯하여 속도대에 따른 기동능력의 변화를 알아둘 필요가 있습니다. 이러한 속도에 따른 기동성능의 변화를 잘 알아볼 수 있게 표시한 것이 E-M 차트(Energy-Maneuver Diagram)입니다. E-M 차트는 특정한 고도를 기준으로 하여, 가로축이 통상 마하수치의 속도, 세로축은 초당 선회율로 이루어집니다.

 E-M 차트는 기본적으로 2개의 수치를 나타내는 차트를 베이스로 하고 있습니다.
 그중 첫 번째는 반비례형태의 G 그래프로써, 주어진 속도(가로축)에서 원하는 선회율(세로축)을 얻기 위해 당겨야 하는 G를 연결한 선을 나타냅니다. 이 그래프를 간단하게 살펴보자면, 같은 속도에서는 더 높은 G를 당기면 더 높은 선회율을 얻을 수 있고, 더 높은 속도일수록 더 높은 G를 당겨야 같은 선회율을 얻을 수 있으며, G가 일정할 때는 더 낮은 속도에서 더 높은 선회율을 얻을 수 있다는 것을 말해주고 있습니다. 위에 있는 속도에 따른 선회율 그래프와 같은 그래프입니다.

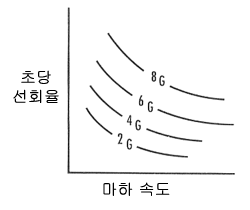
 G 그래프

두 번째는 같은 축에 그려지는 선회반경 그래프입니다. 이를 잠시 살펴보면, 같은 속도에서는 더 좁은 선회반경으로 더 높은 선회율을 얻을 수 있고, 선회율이 같은 경우에는 속도가 높아질수록 선회반경 역시 넓어진다는 것을 보여줍니다. 역시 위의 속도와 G에 따른 선회반경 그래프와 같은 내용이지만, G 그래프와 똑같이 가로축을 마하 속도, 세로축을 초당 선회율로 바꾸어 표시한 것입니다.

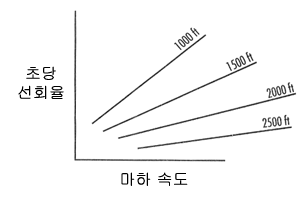
선회반경 그래프

 위의 두 그래프는 정확한 수치를 읽을 수는 없고 단지 개략적인 형태만을 보여주는 것입니다만, 이 두 그래프 자체는 기종에 따라 달라지는 것이 아니라 선회로 인하여 관성을 받는 모든 물체에 근본적으로 동일하게 적용됩니다. 이 두 그래프들은 가로축이 마하 속도, 세로축이 초당 선회율로 동일하므로 하나로 합쳐서 그릴 수가 있고 다음에 보시는 삿갓모양 그래프의 바탕이 됩니다.

다음에 보시는 그래프는 F-16A Block 15형의 특정 고도에서의 E-M차트의 예입니다. 여러분은 이 차트에서 위의 두 그래프가 격자모양으로 엇갈려있는 것을 보실 수 있습니다. 그러나 이 격자모양들은 일정한 영역으로 제한이 되고 있는데, 그것은 대상 기종인 F-16기의 성능의 한계영역 이내에서만 그래프를 나타냈기 때문입니다. 격자선들은 표시된 영역의 바깥으로도 연장될 수 있습니다.

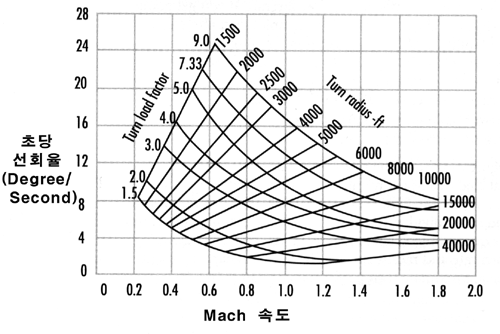
F-16A Block 15형의 일정 고도에서의 E-M 차트

 그래프에 따라서 이 항공기의 비행영역을 설명하자면 다음과 같습니다.

우선, 선회반경 그래프 중 가장 왼쪽의 선은 이 항공기의 최소 선회반경 한계를 나타내며, 여기서는 1500ft입니다. G 그래프중의 가장 위의 선은 이 항공기가 산출할 수 있는 최대 G 한계이며, 여기서는 9G입니다. 또한 이 항공기는 주어진 조건에서 Mach1.8이 최대 속도이므로 그 우측에는 그래프가 존재하지 않으며, 왼쪽 끝은 비행가능한 최저속도입니다. 물론 이 영역한계들은 항공기에 따라 다릅니다. 이 그래프에서는 최대 G를 산출하는 영역 중 최소 속도에서 최대 선회율을 얻을 수 있다는 것도 확연하게 알아볼 수가 있습니다. Y축이 선회율이므로, 가장 위로 뾰족한 지점이 코너속도와 그 때의 최대 선회율입니다. 이 지점의 수치를 읽어보면 대략 Mach 0.6에서 최대 기동성능인 9G로 선회할 수 있고, 이 때 초당 25도의 최대 선회율과 1500피트의 최소선회반경을 얻을 수가 있습니다. 이보다 속도가 높아지면 원심력이 커져서 선회율이 낮아지고, 이보다 낮은 속도에서는 최대 G를 당길 만큼의 양력이 충분하지 못하여 역시 선회율이 낮아집니다.

 코너속도에서 선회율이 최대가 되니까, 코너속도에서 선회를 하면 문제가 풀어질 것 같지요. 그렇지만, 코너속도로 선회하는 것이 기동 역학의 전부가 아닙니다. 양력이 커지면 항력도 커지고 전투기 엔진으로는 이 커진 항력을 보충할 수 없습니다. 즉, 코너속도에서 최대 선회율로 급선회를 하면 속도가 떨어지게 되고, 따라서 당길 수 있는 최대 G도 줄어들게 됩니다. 그러면 결국 선회율이 떨어지게 됩니다. 그렇기 때문에 코너속도에서 얻을 수 있는 최대 선회율은 순간적으로만 얻을 수 있고 선회율은 곧 떨어집니다. 그래서, 코너속도에서 얻을 수 있는 최대 선회율을 그 비행기의 "순간 최대 선회율"이라고 말합니다. 최대 선회율로 선회를 할 때 비행기가 속도를 유지하지 못했던 이유는 높은 G로 기동할 때 항력이 커지고 엔진의 힘으로 이를 보충할 수 없기 때문입니다. 그렇다면, 엔진의 힘으로 보상할 수 있을 정도로 항력을 줄이면 속도가 줄어들지 않고 계속 일정한 G를 유지할 수 있겠지요. 이렇게, 최대 선회율을 포기하고 스틱을 좀 덜 당기는 대신 속도를 유지하면서 선회할 수 있는 능력을 "지속 선회율"이라고 합니다. 공중전에서는 상황에 따라 최대 선회율이 필요할 때도 있고, 지속 선회율이 필요할 때도 있습니다. 일반적으로는, 방어 위치에 있을 때에는 당장 적기의 조준에서 조금이라도 더 벗어나기 위해 에너지를 소모하더라도 최대 선회율로 기동할 필요가 있고, 공격자의 위치에 있을 때에는 적기가 당분간은 당장의 위험이 되지 않으므로 최대 선회율로 기동능력을 한꺼번에 날려 버리지 말고 결정적인 공격찬스를 위해 에너지를 유지하면서 기동하는 것이 좋습니다.

 이와 같이, 같은 비행기가 선회한다고 해서 다 똑같이 선회하는 것이 아닙니다. 어떻게 선회하느냐에 따라 에너지의 유지정도가 달라지고, 그것이 다시 선회능력에 영향을 미칩니다. 이것을 설명하는 것이 잉여추력 개념입니다. 다음 회에서 전투기동에서 매우 중요한 변수의 하나인 잉여추력에 대해서 설명하겠습니다.

 공중전투 메뉴로  |  앞 페이지로  |  맨 위로  |  다음 페이지로